Jonathan Bootle

How to do Zero-Knowledge from Discrete-Logs in under 7kB

We recently had our annual conference for the Academic Centres of Excellence in the UK and I am proud that Jonathan Bootle from UCL won the PhD student elevator pitch competition. I’ll now hand over the rest of the blog post to Jonathan to explain the communication reduction technique for zero-knowledge arguments he presented.

— Jens Groth

In zero-knowledge arguments, a verifier wants to check that a prover possesses secret knowledge satisfying some stated conditions. The prover wants to convince the verifier without disclosing her secrets. Security is based on cryptographic assumptions, like the discrete logarithm assumption. In 1997, Cramer and Damgård produced a discrete log argument requiring the prover to send N pieces of data to the verifier, for a statement of size N. Groth improved this to √N in 2009 and for five years, this was thought to be the best possible. That is, until cryptographers at UCL, including myself, discovered an incredible trick, which shattered the previous record. So how does it work?

dlogzkpic1

The first step is to compile the statement into the correct format for our protocol. Existing compilers take practical statements, such as verifying the correct execution of a C program, and convert them into a type of circuit. We then convert this circuit into a vector equation for the verifier to check. A circuit of size N produces a vector of size roughly N. So far, so good.

dlogzkpic2

We also need use a commitment scheme, which works like a magician’s envelope. By committing to a hidden value, it can be fixed, and revealed later.

dlogzkpic3

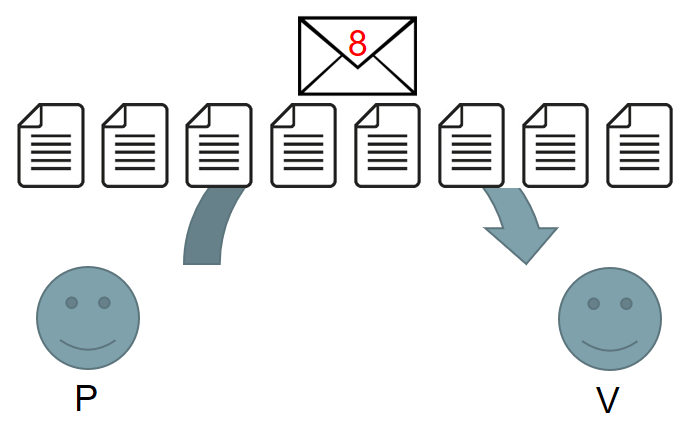
In previous works in the discrete logarithm setting, the prover commits to the vector using a single commitment.

dlogzkpic4

Later the prover reveals the whole vector. This gives high communication costs, and was a major bottleneck.

dlogzkpic5

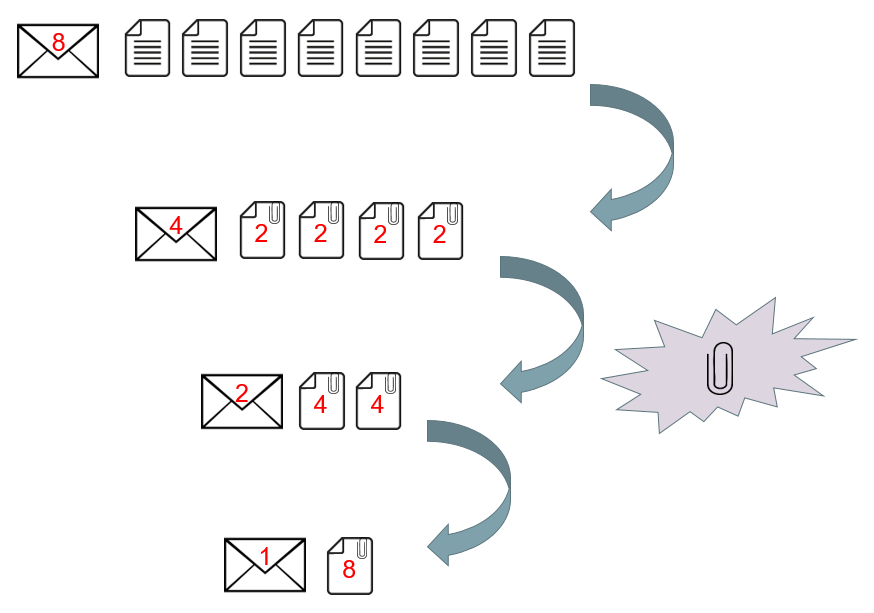
We discovered a rare and extraordinary property of the commitment scheme which allowed us to cut a vector in half and compress the two halves together. Applying the same trick repeatedly produces a single value which is easy to send, and drastically reduces the communication costs of the protocol.

dlogzkpic6

We begin with a vector of roughly N elements. If we repeatedly cut the vector in half, it takes log(N) cuts to produce a vector containing only a single element. Each time that the prover cuts a vector in half, they must make new commitments to enable the verifier to check the shorter vectors produced. Overall, roughly log(N) new commitments are produced, so the prover must send about log(N) values to the verifier. This is a dramatic improvement from √N. To put this in perspective, doubling the size of the statement only adds a constant amount of data for the prover to send.

Of course, it is possible to base security on other cryptographic assumptions, but other efficient protocols often use very strong and untested assumptions which have yet to receive a high level of scrutiny. By contrast, the discrete logarithm assumption has been used and studied for over three decades.

Is this just a theoretical advance? Far from it. Our protocol has a working Python implementation, which has been extensively benchmarked. By combining our code with the compilers that I mentioned earlier, we verified the correct execution of C programs. By sending under 7kB of data each time, we can verify matrix multiplications, simulations of the motion of gas molecules, and SHA-1 hashes. It’s nice to see theory that compiles and works.

 

The full paper is by Jonathan Bootle, Andrea Cerulli, Pyrros Chaidos, Jens Groth and Christophe Petit and was published at EUROCRYPT 2016.

Workshop: Theory and Practice of Secure Multiparty Computation

Members of the UCL information security group visiting Aarhus rainbow panorama.
Members of the UCL information security group visiting the Aarhus rainbow panorama

The workshop was organized by CFEM and CTIC, and took place in Aarhus from May 30 until June 3, 2016. The speakers presented both theoretical advancements and practical implementations (e.g., voting, auction systems) of MPC, as well as open problems and future directions.

The first day started with Ivan Damgård presenting TinyTable, a new simple 2-party secure computation protocol. Then Martin Hirt introduced the open problem of general adversary characterization and efficient protocol generation. The last two talks of the day discussed Efficient Constant-Round Multiparty Computation and Privacy-Preserving Outsourcing by Distributed Verifiable Computation.

The first session of the second day included two presentations on theoretical results which introduced a series of three-round secure two-party protocols and their security guarantees, and fast circuit garbling under weak assumptions. On the practical side, Rafael Pass presented formal analysis of the block-chain, and abhi shelat outlined how MPC can enable secure matchings. After the lunch break, probabilistic termination of MPC protocols and low-effort VSS protocols were discussed.

Yuval Ishai and Elette Boyle kicked off the third day by presenting constructions of function secret sharing schemes, and recent developments in the area. After the lunch break, a new hardware design enabling Verifiable ASICs was introduced and the latest progress on “oblivious memories” were discussed.

The fourth day featured presentations on RAMs, Garbled Circuits and a discussion on the computational overhead of MPC under specific adversarial models. Additionally, there was a number of presentations on practical problems, potential solutions and deployed systems. For instance, Aaron Johnson presented a system for private measurements on Tor, and Cybernetica representatives demonstrated Sharemind and their APIs. The rump session of the workshop took place in the evening, where various speakers were given at most 7 minutes to present new problems or their latest research discoveries.

On the final day, Christina Brzuska outlined the connections between different types of obfuscation and one-way functions, and explained why some obfuscators were impossible to construct. Michael Zohner spoke about OT extensions, and how they could be used to improve 2-party computation in conjunction with look-up tables. Claudio Orlandi closed the workshop with his talk on Amortised Garbled Circuits, which explained garbling tricks all the way from Yao’s original work up to the state of the art, and provided a fascinating end to the week.